BALANCED_ROBOT
参考文献
倒立摆系统
LQR及观测器简介
平衡步兵
首都师范共轴麦轮
哈工程轮腿
上交轮腿
合工大轮腿仿真
达妙科技轮腿
中南打滑检测
1.倒立摆系统
倒立摆是机器人学中一个非常重要的模型,火箭、导弹、独轮车、双足机器人、四足机器人、两轮自平衡机器人、轮腿机器人,基本都是倒立摆的变形。
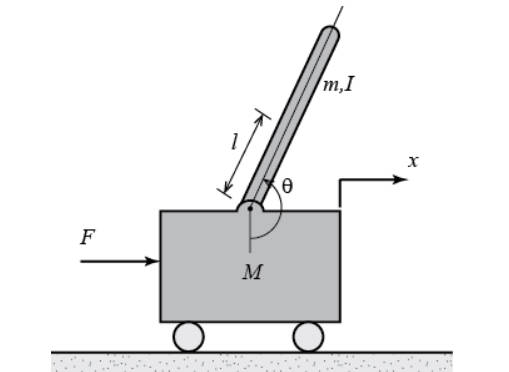
本章提到的倒立摆系统为一阶倒立摆,不考虑阻尼,以下为本章用到的物理参数
| 参数符号 | 参数含义 | 参数单位 |
|---|---|---|
| 施加在滑块上的作用力 | ||
| 滑块的位移 | ||
| 摆杆质心的位移 | ||
| 摆杆长度的一半 | ||
| 滑块的质量 | ||
| 摆杆的质量 | ||
| 摆杆与竖直方向的夹角 | ||
| 摆杆的转动惯量( |
1.1拉格朗日动力学
所谓动力学不过是通过一种方法求出力与运动之间的关系,对于拉格朗日动力学来说,若要求系统中的力或者力矩就可以使用以下动力学方程:
式中
- 若操作机的执行元件控制某个转动变量
时,则执行元件的总力矩 应为:
- 若操作机的执行元件控制某个移动变量
时,则施加在运动方向 上的力应为:
若某个关节不存在外加作用力,即力学系统所受的主动力全是保守力时,式
式中:
1.2状态空间方程推导
设坐标原点为转轴,可得摆杆质心位移:
则倒立摆摆杆质心速度:
摆杆的平动动能可由式
即:
系统总势能只受摆杆位置的影响,可得:
由式
针对移动变量
求解拉格朗日方程可得:
为了对系统进行线性分析和控制,需要对上述的非线性系统在在平衡点附近进行线性化。系统平衡点附近时,倒立摆的摆角
从而得到一阶倒立摆系统在平衡点附近的线性化模型为:
已知
根据方程组
式中:
1.3LQR控制器
对于 lqr 函数,即可得到系统
矩阵中对角线上的各元素值越大,其所对应的状态变量的响应速度越快,对系统的影响程度越大,而其他状态变量的响应速度就会变慢,对系统的影响也会削弱。 矩阵不能太小,否则会导致控制量增大,而超出系统执行的能力。 阵也不要太大,否则导致控制量太小,而影响控制性能。 - 由于控制模型为线性化模型,所以
的选取应该使系统各状态工作线性范围之内。
本章更关注机器人稳摆速度,所以
clear;
clc;
%% 定义倒立摆物理性质
M = 2; % 滑块质量
m = 0.1; % 摆杆质量
l = 0.5; % 摆杆长度的一半
g = 9.81; % 重力加速度
%% 状态空间矩阵
A = [0 0 1 0;
0 0 0 1;
0 -3*m*g/(4*M+m) 0 0;
0 3*(M+m)*g/((4*M+m)*l) 0 0];
B = [0;0;4/(4*M+m);-3/((4*M+m)*l)];
%% 求LQR增益矩阵
Q = diag([100 100 10 10]); % x q dx dq
R = 1; % fx
K = lqr(A,B,Q,R);
disp('K = ');
disp(K);得到
1.4牛顿力学法
机器人的动力学和运动学模型是实现机器人控制策略的基础。想要完成对自平衡机器人控制系统的设计,需要根据自平衡机器人的运动特点和结构特点进行分析,建立准确可靠的数学模型。机器人动力学建模有两种具有代表性的方法:牛顿力学法和拉格朗日函数法。
- 拉格朗日函数法依据
原理,利用标量代替矢量,对总动量和总势能进行分析,建立动力学模型。这种方法运用能量方式建模,不需要对内向力进行分析。 - 牛顿力学法运用牛顿定律和动量矩定理对各部分刚体的受力情况进行隔离分析,然后建立相邻刚体间的内力项,最终得到系统的动力学模型。牛顿力学建模法可以表达出系统完整的受力关系,有明确的物理意义,该方法建立的模型易于被控对象控制策略的设计。
本章将采用牛顿力学法重新推导前文倒立摆系统的状态空间方程
分析滑块在水平方向上受力平衡,可得:
分析摆杆在水平方向上受力平衡,可得:
即:
分析摆杆在竖直方向上受力平衡,可得:
即:
分析摆杆绕其质心的力矩平衡,可得:
倒立摆稳摆时的摆角
可得局部线性化动态模型:
式
2.两轮自平衡机器人系统
两轮自平衡机器人系统是一阶倒立摆系统的一种变形,即将滑块改为驱动轮 ,摆杆改为小板凳本体,作用在滑块上的驱动力
| 参数符号 | 参数含义 | 参数单位 |
|---|---|---|
| 左右驱动轮的输出转矩 | ||
| 本体质心的位移 | ||
| 左右驱动轮的位移 | ||
| 两驱动轮轴中心的位移 | ||
| 本体的俯仰角 | ||
| 本体的偏航角 | ||
| 左右驱动轮的转角 | ||
| 本体的质量 | ||
| 左右驱动轮的质量 | ||
| 左右驱动轮的半径 | ||
| 左右驱动轮之间的距离 | ||
| 本体重心与驱动轮轮轴之间的距离 | ||
| 左右驱动轮的转动惯量( | ||
| 本体绕 | ||
| 本体绕 |
由于机器人的控制是非线性的,难以精确地去建立其数学模型,所以为了建立可行性较高的系统模型,我们进行如下假设:
- 两轮自平衡机器人各部件均为刚体;
- 忽略两轮自平衡机器人受到的外界干扰力;
- 忽略两轮自平衡机器人本体和两驱动轮转轴之间的摩擦力;
- 两驱动轮与地面没有相对滑动
2.1拉格朗日函数法
两轮自平衡机器人位移和速度与左右驱动轮转角和角速度的转化关系如下:
右轮同理,得:
两轮自平衡机器人偏航角和偏航角速度与左右驱动轮转角和角速度的转化关系如下:
此外,结构本体质心位移和速度与两轮轴中心的位移和速度的关系满足:
左右驱动轮的平均动能:
左右驱动轮绕
本体质心的平动动能:
本体绕
本体绕
系统总动能:
将式
欲使系统具有确定运动,则需保证确定系统位置的独立参数的个数等于系统的自由度数。两轮自平衡机器人在平面运动时具有三个自由度。所以选取左驱动轮转角
选用左右驱动轮的转角
在此坐标系下,相应的广义力
由式
该动力学模型具有复杂的非线性、多变性和强耦合性。为了进一步深入研究两轮自平衡机器人的特性,本章基于以下假设对两轮自平衡机器人的非线性动力学模型进行线性化:
- 当本体倾角
在平衡点附件小范围变化时,假设:
- 本体绕垂直方向轴的转动惯量
与 有关。当俯仰角 在两轮自平衡机器人平衡点附近小范围内变化时,为了简化计算,假设 为常值; - 假设两驱动轮尺寸一致,车轮始终保持与地面接触,忽略内部能量损耗
基于以上假设,取:
解得该两轮自平衡机器人的动力学模型为:
式
式
式
联立约束式
其中:
MATLAB脚本为:
clear;
clc;
%% 定义小车倒立摆物理性质
R = 0.07625; %车轮的半径
D = 0.31; %左轮、右轮两个轮子间的距离
l = 0.05; %摆杆质心到转轴距离
m = 0.741 * 2; %车轮的质量, 共轴麦轮为两个轮的质量
M = 4.886; %摆杆质量
I = (1/2)*m*R^2; %车轮的转动惯量
Jy = (1/3)*M*l^2; %机器人机体对 y 轴的运动时产生的转动惯量(俯仰方向)
Jz = (1/12)*M*D^2; %机器人机体对 z 轴的运动时产生的转动惯量(偏航方向)
g = 9.8; %重力加速度
%% 状态空间矩阵
Q_eq = Jy*M + (Jy+M*l^2) * (2*m+(2*I)/R^2);
% A为系统矩阵
A_23=-(M^2*l^2*g)/Q_eq;
A_43=M*l*g*(M+2*m+(2*I/R^2))/Q_eq;
A = [0 1 0 0 0 0;
0 0 A_23 0 0 0;
0 0 0 1 0 0;
0 0 A_43 0 0 0;
0 0 0 0 0 1;
0 0 0 0 0 0;];
% B为输入矩阵
B_21=(Jy+M*l^2+M*l*R)/Q_eq/R;
B_22 = B_21;
B_41=-((M*l/R)+M+2*m+(2*I/R^2))/Q_eq;
B_42 = B_41;
B_61 = -D/(D^2*(M*R+I/R)+2*Jz*R);
B_62 = -B_61;
B = [0 0;
B_21 B_22;
0 0;
B_41 B_42;
0 0;
B_61 B_62];
% C为输出矩阵
C = eye(6);
D = 0;
%% 求LQR增益矩阵
Q = diag([0.001 4 8 0.8 4 0.8]);
R = diag([1 1]);
K = lqr(A, B,Q,R);
disp('K = ');
disp(K);建模如下图 
2.2牛顿力学法
为了便于两轮自平衡机器人系统牛顿力学法的分析,现在原基础上定义以下物理参数
| 参数符号 | 参数含义 | 参数单位 |
|---|---|---|
| 左右驱动轮受到地面的摩擦力 | ||
| 左右驱动轮受到车体作用力的水平分力 | ||
| 左右驱动轮受到车体作用力的竖直分力 |
车轮的运动可分解为平动和转动,则由牛顿第二定律可得:
由刚体定轴转动定律可得:
联立式
对左轮也同理:
式
对车体,水平方向上有:
即:
竖直方向上有:
即:
对车体,由刚体定轴转动定律可得:
联立式
联立式
当本体倾角
代入式
联立式
转向运动是由于左右两车轮从水平方向上施加给车体的反作用力的大小
式
式
3.轮腿式平衡机器人系统(哈工程模型)
3.1平衡与纵向运动控制
3.1.1模型定义
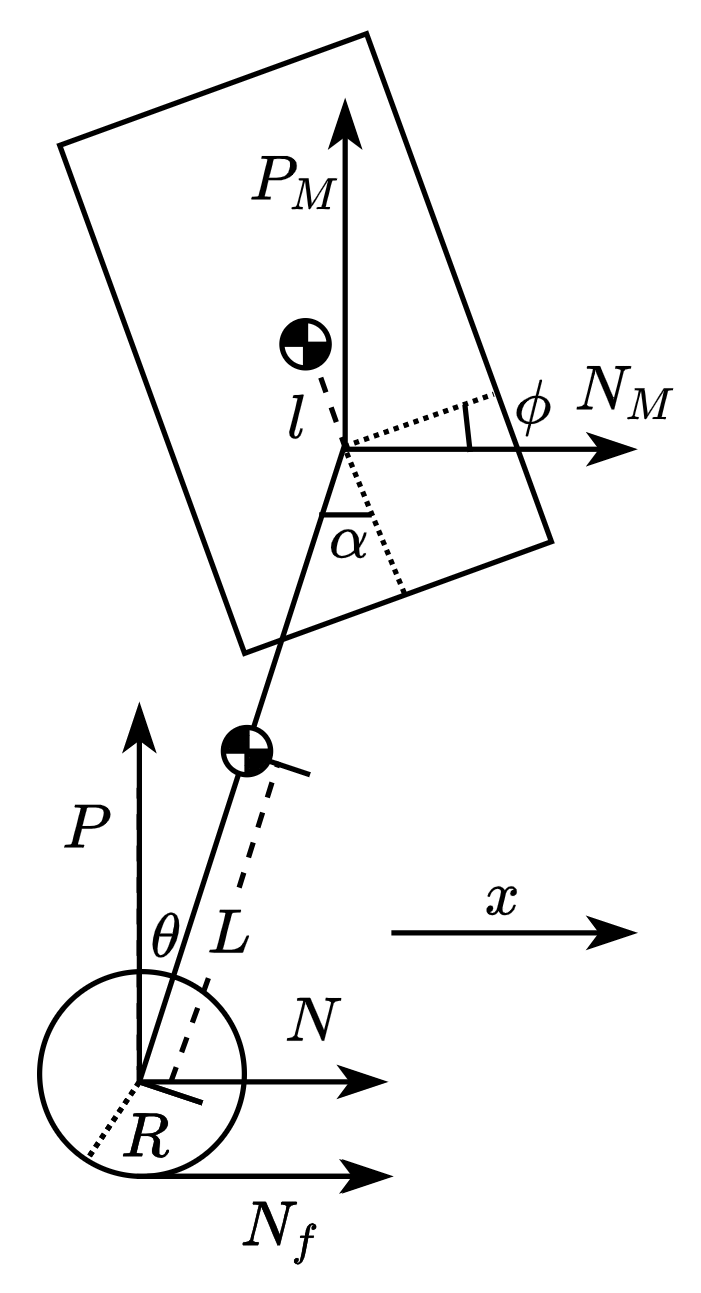
| 参数符号 | 参数含义 | 参数单位 |
|---|---|---|
| 摆杆与竖直方向夹角 | ||
| 机体与水平夹角 | ||
| 摆杆与机体相对角度 | ||
| 驱动轮位移 | ||
| 驱动轮输出力矩 | ||
| 髋关节输出力矩 | ||
| 驱动轮对摆杆力的水平分量 | ||
| 驱动轮对摆杆力的竖直分量 | ||
| 地面对驱动轮摩擦力 | ||
| 摆杆对机体力水平方向分量 | ||
| 摆杆对机体力竖直方向分量 | ||
| 摆杆推力 | ||
| 驱动轮半径 | ||
| 摆杆重心到驱动轮轴距离 | ||
| 摆杆重心到机体转轴距离 | ||
| 机体重心到其转轴距离 | ||
| 驱动轮转子质量 | ||
| 摆杆质量 | ||
| 机体质量 | ||
| 驱动轮转子转动惯量 | ||
| 摆杆绕质心转动惯量 | ||
| 机体绕质心转动惯量 |
3.1.2经典力学分析
车轮的运动可分解为平动和转动,则由牛顿第二定律可得:
由刚体定轴转动定律可得:
联立式
对摆杆,水平方向上有:
竖直方向上有:
由刚体定轴转动定律可得:
对机体,水平方向上有:
竖直方向上有:
由刚体定轴转动定律可得:
3.1.3状态空间方程及LQR控制器
定义:
利用MATLAB符号运算工具,根据式 solve对式
function K = get_k_length(leg_length)
%theta : 摆杆与竖直方向夹角 R :驱动轮半径
%x : 驱动轮位移 L : 摆杆重心到驱动轮轴距离
%phi : 机体与水平夹角 LM : 摆杆重心到其转轴距离
%T :驱动轮输出力矩 l : 机体重心到其转轴距离
%Tp : 髋关节输出力矩 mw : 驱动轮转子质量
%N :驱动轮对摆杆力的水平分量 mp : 摆杆质量
%P :驱动轮对摆杆力的竖直分量 M : 机体质量
%Nm :摆杆对机体力水平方向分量 Iw : 驱动轮转子转动惯量
%Pm :摆杆对机体力竖直方向分量 Ip : 摆杆绕质心转动惯量
%Nf : 地面对驱动轮摩擦力 Im : 机体绕质心转动惯量
syms x(t) T R Iw mw M L LM theta(t) l phi(t) mp g Tp Ip IM
syms f1 f2 f3 d_theta d_x d_phi theta0 x0 phi0
%% 定义数值变量
R1=0.0603; %驱动轮半径
L1=leg_length/2; %摆杆重心到驱动轮轴距离
LM1=leg_length/2; %摆杆重心到其转轴距离
l1=0.011; %机体质心距离转轴距离
mw1=0.6; %驱动轮质量
mp1=0.045; %杆质量
M1=1.44; %机体质量
Iw1=0.5*mw1*R1^2; %驱动轮转动惯量
Ip1=mp1*((L1+LM1)^2+0.048^2)/12.0; %摆杆转动惯量,视为长方体
IM1=M1*(0.135^2+0.066^2)/12.0; %机体绕质心转动惯量,视为长方体
%% 定义运动方程
NM = M*diff(x + (L + LM )*sin(theta)-l*sin(phi),t,2);
N = NM + mp*diff(x + L*sin(theta),t,2);
PM = M*g + M*diff((L+LM)*cos(theta)+l*cos(phi),t,2);
P = PM +mp*g+mp*diff(L*cos(theta),t,2);
eqn1 = diff(x,t,2) == (T-N*R)/(Iw/R + mw*R);
eqn2 = Ip*diff(theta,t,2) == (P*L + PM*LM)*sin(theta)-(N*L+NM*LM)*cos(theta)-T+Tp;
eqn3 = IM*diff(phi,t,2) == Tp +NM*l*cos(phi)+PM*l*sin(phi);
% 通过替换变量简化运动方程,主要是将方程中对时间t求导的符号变量替换为其他辅助变量
eqn10 = subs(eqn1,[diff(theta,t,2),diff(x,t,2),diff(phi,t,2),diff(theta,t),diff(x,t),diff(phi,t),theta,x,phi],[f1,f2,f3,d_theta,d_x,d_phi,theta0,x0,phi0]);
eqn20 = subs(eqn2,[diff(theta,t,2),diff(x,t,2),diff(phi,t,2),diff(theta,t),diff(x,t),diff(phi,t),theta,x,phi],[f1,f2,f3,d_theta,d_x,d_phi,theta0,x0,phi0]);
eqn30 = subs(eqn3,[diff(theta,t,2),diff(x,t,2),diff(phi,t,2),diff(theta,t),diff(x,t),diff(phi,t),theta,x,phi],[f1,f2,f3,d_theta,d_x,d_phi,theta0,x0,phi0]);
%% 求状态空间矩阵
% 求解由eqn10、eqn20和eqn30方程组成的三元一次代数方程组,并将解赋值给符号变量f1、f2和f3
[f1,f2,f3] = solve(eqn10,eqn20,eqn30,f1,f2,f3);
% 求解状态方程,并在系统的平衡点处线性化系统
A=subs(jacobian([d_theta,f1,d_x,f2,d_phi,f3],[theta0,d_theta,x0,d_x,phi0,d_phi]),[theta0,d_theta,d_x,phi0,d_phi,T,Tp],[0,0,0,0,0,0,0]);
% 将符号变量替换为数值变量,求解状态方程数值解
AA=subs(A,[R,L,LM,l,mw,mp,M,Iw,Ip,IM,g],[R1,L1,LM1,l1,mw1,mp1,M1,Iw1,Ip1,IM1,9.8]);
AA=double(AA);
% 求解状态方程,并在系统的平衡点处线性化系统
B=subs(jacobian([d_theta,f1,d_x,f2,d_phi,f3],[T,Tp]),[theta0,d_theta,d_x,phi0,d_phi,T,Tp],[0,0,0,0,0,0,0]);
% 将符号变量替换为数值变量,求解状态方程数值解
BB=subs(B,[R,L,LM,l,mw,mp,M,Iw,Ip,IM,g],[R1,L1,LM1,l1,mw1,mp1,M1,Iw1,Ip1,IM1,9.8]);
BB=double(BB);
%% 求LQR增益矩阵
Q=diag([1 0.07 10 5 300 0.6]);
R=[20 0;0,1]; %T Tp
K=lqr(AA,BB,Q,R);
end由于表达式较为复杂所占篇幅较大,此处用符号代替。 
3.2五连杆运动学解算与VMC
3.2.1正运动学解算
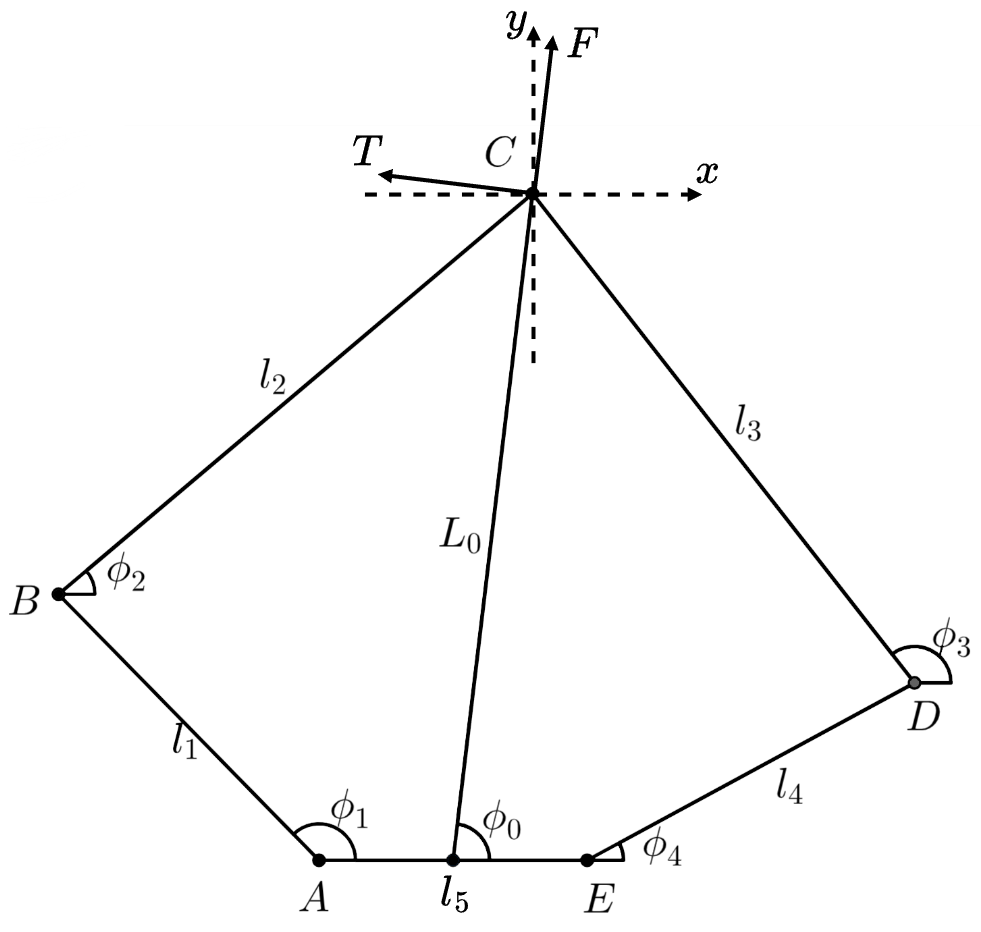 五连杆机构参数定义如图所示,其中
五连杆机构参数定义如图所示,其中
定义
对其移项,并在等式两边进行平方,有:
两式相加可得:
将原式变形为:
已知:
使用二倍角公式对原式进行展开并化简得到一个关于
其解为:
其中:
得到角度
极坐标为:
3.2.2VMC雅可比矩阵
定义:
对正运动学模型
即:
雅可比矩阵
有:
即通过雅可比矩阵
定义:
根据虚功原理,有:
将式
综上通过正运动学模型雅可比矩阵即可解算出关节电机输出力矩。 但对上文推导出的正运动学模型直接求取雅可比矩阵
其中
消去
其中:
将
利用 MATLAB 进行符号运算,得:
3.3观测器设计
使用卡尔曼滤波融合IMU加速度计与电机编码器,对机体姿态进行估计,以应对踩小弹丸一类的打滑场景
具体代码实现请看
3.4打滑检测
| 参数符号 | 参数含义 | 参数单位 |
|---|---|---|
| 摆杆与竖直方向夹角 | ||
| 左右连杆等效腿长 | ||
| 轮毂的转速 | ||
| 轮半径 | ||
| 机体宽度 | ||
| 上层机体平移速度 | ||
| 轮胎与地面接触点的绝对速度(滑动速度) | ||
| 地面接触点相对于轮毂轴心的速度 | ||
| 轮毂轴心相对于机体的速度 | ||
| 上层机体旋转产生的附加速度 |
在比赛场上非常有必要分析平衡机器人的打滑状态并做出调整,否则很容易翻车倒地,下面对经典力学防打滑的分析,检测平衡两轮毂与地面接触点的速度差值,当这个差值超过某个阈值时判定为打滑,下面求该速度差值:
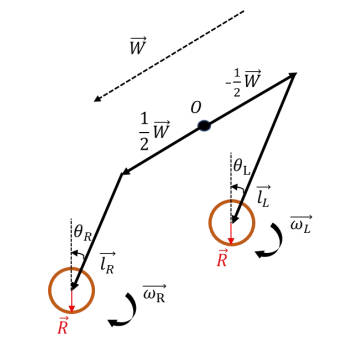
右连杆地面接触点速度:
地面接触点相对于右轮毂轴心的速度:
轮毂轴心相对于机体的位移差为:
因此右轮轴心相对于机体的速度向量为:
右侧地面接触点因机体横滚、俯仰、偏航而产生的附加速度向量为:
同理 左连杆地面接触点速度:
地面接触点相对于左轮毂轴心的速度:
左轮轴心相对于机体的速度向量为:
左侧地面接触点因机体横滚、俯仰、偏航而产生的附加速度向量为:
速度差值为:
当速度差值的大小
4.说明
- 本文所有的公式推导与建模都基于右手系,本文
轴为机体前进正方向, 轴竖直向上 - 本文的姿态角均以右手系各轴的逆时针方向为正方向,
对应 轴, 对应 轴, 对应 轴,以 为例,绕 轴逆时针旋转, 值增加,且角速度为正值