神经网络

线性回归

即线性神经网络，是最简单的一种形式

线性回归很好理解，可自行阅读该内容

提示

理解并简单复现文中代码

多层感知机

线性模型可能会出错

线性意味着单调假设：任何特征的增大都会导致模型输出的增大或减小

有时这是有道理的，例如如果我们试图预测一个人是否会偿还贷款，我们可以认为，收入较高的人更有可能偿还贷款。但是，虽然收入与还款概率存在单调性，但它们不是线性相关的。收入从0增加到5万，可能比从100万增加到105万带来更大的还款可能性

然而我们可以很容易找出违反单调性的例子。例如，我们想要根据体温预测死亡率，对体温高于37摄氏度的人来说，温度越高风险越大，但对体温低于37摄氏度的人来说，温度越高风险就越低

但是，如何对猫和狗的图像进行分类呢？增加某处像素的强度是否总是增加（或降低）图片是狗的可能性？对线性模型的依赖对应于一个隐含的假设，即区分猫和狗的唯一要求是评估单个像素的强度。在一个把图像倒过来不会改变类型的世界里，这种方法注定会失败

与前面的例子相比，很难说这里的线性关系成立。任何像素的重要性都以复杂的方式取决于该像素周围像素的值。数据可能会有一种表示方式，在基础上建立一个线性模型可能会是合适的，但我们不知道如何手动计算。对于深度神经网络，我们使用观测数据来联合学习隐藏层表示和应用于该表示的线性预测器

从单层到多层

我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制，处理更普遍的函数关系

要做到这一点，最简单的方法是将许多层堆叠在一起，每一层都输出到上面的层，直到生成最后的输出

我们把前面的所有层看作表示，把最后一层看作线性预测器，这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP

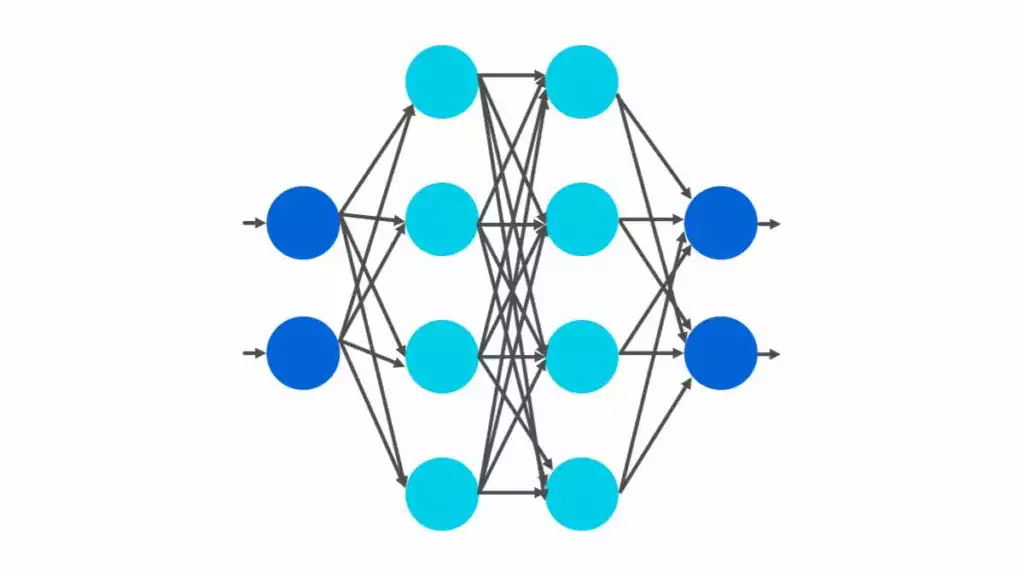
例如图中的这个多层感知机有2个输入，2个输出，其隐藏层包含2层共8个隐藏单元

输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算，因此这个多层感知机的层数为3

全连接层

这几个层都是全连接的，每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元

这样的网络结构非常简单，但全部由全连接层组成的多层感知机，运行时参数需要的性能开销可能会非常高，因此在CNN和RNN等技术中会采用其他的形式的层来提高推理速度

提示

可自行了解卷积层、池化层等概念

任务

完成任务10，想往这方面深入研究的，可以去学一下PyTorch或者TensorFlow，此外还有mxnet和百度的paddle等可选，但明显不如torch和tf流行